George W. Taylor, 22 May 2011
🔗 Update (2025): A significantly expanded and refined treatment of these ideas appears in my new paper:
Uncovering the Structural Geometry of Permutations (2025)
Many computationally efficient methods have been devised to solve the problem of visiting all n! permutations of some given set of n digits to keep the run time to a minimum. We present a simple meta algorithm that can enhance the efficiency of permutation production with many of these methods in limited circumstances.
The rule to determine the number of permutations of n objects was known in Hindu culture at least as early as around 1150. One classical algorithm based on finding the next permutation in lexicographic ordering goes back to Narayana Pandita in 14th century India.
Here is that algorithm in C. You will note that it requires over 20 lines of code to generate each permutation. In recent decades, computational methods have advanced well beyond that ancient algorithm. Indeed, Knuth describes many algorithms dedicated to efficient permutation generation in his book "The Art of Computer Programming". This paper describes yet another. It is actually a meta algorithm, since it describes a method to reduce the number of times one needs to call upon a permutation generation function in the first place, whichever is used. Instead, frequently next permutation in the sequence can be derived from a single operation using a simple table. This algorithm is applicable to generating all permutations for a given set, given a sequence of elements (a0, a1, a2, ..., an-1), initially sorted so that (a0 < a1 < a2, ... < an-1).
The algorithm was inspired by the observation that the differences between successive ordered permutations follows a fractal pattern. Specifically, the table of differences for the first 1/2n! is mirrored in the second half. A second observation is that any given table recapitulates the set of differences for each successively smaller factorial. Each of these subsets also have the same mirrored symmetry between the first half and the second half. Thus it is only necessary to generate the first half of each, and employ the differences between successive permutations generated to calculate the second half by adding the appropriate difference to derive each next permutation.
One will employ any one of the permutation generating algorithms along side this algorithm as long as it visits the permutations in lexicographical order. What this algorithm does is reduce the need to call upon a permutation generating algorithm to significantly less than half the time, replacing it with a single operation to generate the next permutation instead. The value to add is fetched from an (optional) table created by storing the difference between the current permutation and the previous permutation as they are generated. These values are only calculated and stored for half the total number of permutations. A very different method will also be discussed, also inspired by the observations below.
The following discussion assumes the customary base 10 numbering system and digits stored in an array. This algorithm, however, also works with numbers of any base bit-packed into an integer. In this case, actual values will be different than those shown, but the patterns will be the same.
Given the set of 3 digits (0,1,2), there are 6 permutations. In lexicographical order: 012, 021, 102, 120, 201, 210. Subtracting the first from the second gives 9, subtracting the second from the third gives 81, and subtracting the third from the fourth gives 18, etc, such that we generate the series 9, 81, 18, 81, 9. The symmetry is obvious here. The first half of the table: 9, 81 is mirrored in the last half: 81, 9. One only needs to generate the first half of the table plus one to get 012, 021, 102 then add 18 to the previous 102 to get the next - 120, add 81 to that to get the next - 201, and finally add 9 to get the last - 210.
Let us examine the set of 4 digits. Subtracting one permutation from the next in sequence, we can compute a table of differences that shows us its symmetry. You will note that the first group of 5 values are identical with the table for the 3 digit set above, which is followed by 13 values unique to the set of permutations for 4 digits, then followed again by the table for the 3 digit set. You can plainly see that the table reads the same from bottom to top as it does from top to bottom.
0: 0123 diff: n/a
from 3 digit permutations
1: 0132 diff: 9
2: 0213 diff: 81
3: 0231 diff: 18
4: 0312 diff: 81
5: 0321 diff: 9
-----------------
6: 1023 diff: 702
7: 1032 diff: 9
8: 1203 diff: 171
9: 1230 diff: 27
10: 1302 diff: 72
11: 1320 diff: 18
12: 2013 diff: 693 <---centre of symmetry
13: 2031 diff: 18
14: 2103 diff: 72
15: 2130 diff: 27
16: 2301 diff: 171
17: 2310 diff: 9
18: 3012 diff: 702
------------------
from 3 digit permutations
19: 3021 diff: 9
20: 3102 diff: 81
21: 3120 diff: 18
22: 3201 diff: 81
23: 3210 diff: 9
Then using our algorithm, one would employ their preferred permutation generating algorithm to generate the first 3 permutations, then add the differences as described above to produce the last 2 values of the first group. Then once more one call upon the permutation generating algorithm to produce the next 7 permutations. Finally, one can use the values derived from subtracting subsequent values from the first half of the table to generate the last half. In total, 23 calls to the permutation generating algorithm have been reduced to 10. The rest of the permutations have been generated by simply adding the appropriate difference to successive permutations.
Here is the anatomy of the table of differences for the permutations of a set of 5 digits. It begins to reveal the fractal nature of its structure. Not only do we see that the first group of 5 differences is the same as you would get from the set of permutations of a 3 digit set, and that the next group of 23 differences is the same as you would get from the set of permutations of a 4 digit set, but also, within the central body of differences we see echos of these other sets. More of these are revealed as we generate tables for bigger and bigger sets, indicating that there are other savings in computations to be gained if the full fractal nature can be captured in an algorithm.
0: 01234 diff: n/a
from 4 digit permutations
from 3 digit permutations
1: 01243 diff: 9
2: 01324 diff: 81
3: 01342 diff: 18
4: 01423 diff: 81
5: 01432 diff: 9
end 3 digit permutations
6: 02134 diff: 702
7: 02143 diff: 9
8: 02314 diff: 171
9: 02341 diff: 27
10: 02413 diff: 72
11: 02431 diff: 18
12: 03124 diff: 693
13: 03142 diff: 18
14: 03214 diff: 72
15: 03241 diff: 27
16: 03412 diff: 171
17: 03421 diff: 9
18: 04123 diff: 702
from 3 digit permutations
19: 04132 diff: 9
20: 04213 diff: 81
21: 04231 diff: 18
22: 04312 diff: 81
23: 04321 diff: 9
end 3 digit permutations
end 4 digit permutations
24: 10234 diff: 5913
from 3 digit permutations
25: 10243 diff: 9
26: 10324 diff: 81
27: 10342 diff: 18
28: 10423 diff: 81
29: 10432 diff: 9
end 3 digit permutations
30: 12034 diff: 1602
31: 12043 diff: 9
32: 12304 diff: 261
33: 12340 diff: 36
34: 12403 diff: 63
35: 12430 diff: 27
36: 13024 diff: 594
37: 13042 diff: 18
38: 13204 diff: 162
39: 13240 diff: 36
40: 13402 diff: 162
41: 13420 diff: 18
42: 14023 diff: 603
--------------------
43: 14032 diff: 9
44: 14203 diff: 171
45: 14230 diff: 27 chunk from upper half of the centre of 4 digits
46: 14302 diff: 72
47: 14320 diff: 18
--------------------
48: 20134 diff: 5814
--------------------
49: 20143 diff: 9
50: 20314 diff: 171
51: 20341 diff: 27 chunk from upper half of the centre of 4 digits
52: 20413 diff: 72
53: 20431 diff: 18
-------------------
54: 21034 diff: 603
55: 21043 diff: 9
56: 21304 diff: 261
57: 21340 diff: 36
58: 21403 diff: 63
59: 21430 diff: 27
60: 23014 diff: 1584---centre of symmetry
61: 23041 diff: 27
62: 23104 diff: 63
63: 23140 diff: 36
64: 23401 diff: 261
65: 23410 diff: 9
66: 24013 diff: 603
--------------------
67: 24031 diff: 18
68: 24103 diff: 72
69: 24130 diff: 27 chunk from lower half of the centre of 4 digits
70: 24301 diff: 171
71: 24310 diff: 9
--------------------
72: 30124 diff: 5814
--------------------
73: 30142 diff: 18
74: 30214 diff: 72
75: 30241 diff: 27 chunk from lower half of the centre of 4 digits
76: 30412 diff: 171
77: 30421 diff: 9
--------------------
78: 31024 diff: 603
79: 31042 diff: 18
80: 31204 diff: 162
81: 31240 diff: 36
82: 31402 diff: 162
83: 31420 diff: 18
84: 32014 diff: 594
85: 32041 diff: 27
86: 32104 diff: 63
87: 32140 diff: 36
88: 32401 diff: 261
89: 32410 diff: 9
90: 34012 diff: 1602
from 3 digit permutations
91: 34021 diff: 9
92: 34102 diff: 81
93: 34120 diff: 18
94: 34201 diff: 81
95: 34210 diff: 9
end 3 digit permutations
96: 40123 diff: 5913
from 4 digit permutations
from 3 digit permutations
97: 40132 diff: 9
98: 40213 diff: 81
99: 40231 diff: 18
100: 40312 diff: 81
101: 40321 diff: 9
end 3 digit permutations
102: 41023 diff: 702
103: 41032 diff: 9
104: 41203 diff: 171
105: 41230 diff: 27
106: 41302 diff: 72
107: 41320 diff: 18
108: 42013 diff: 693
109: 42031 diff: 18
110: 42103 diff: 72
111: 42130 diff: 27
112: 42301 diff: 171
113: 42310 diff: 9
114: 43012 diff: 702
from 3 digit permutations
115: 43021 diff: 9
116: 43102 diff: 81
117: 43120 diff: 18
118: 43201 diff: 81
119: 43210 diff: 9
end 3 digit permutations
end 4 digit permutations
Finally, we come to the algorithm itself...
The table of differences for all n! permutations of the set (0, 1, 2, 3, 4, ..., n-1) includes at its start the table of differences for all (n-1)! permutations and that table contains at its start the table of differences all (n-2)! permutations and so on and so on until we find that the first 5 differences in any table are equal to the difference table for 3! (which itself begins with the single difference '9' of the 2! permutations of the set (0,1), but we will ignore that and begin with 3!)
As we said, to produce the permutations for a set of 4 digits, we first created the subset for 3. The pattern here then can be said to be "3,4". To generate the permutations of the set of 5 digits, we must first create the table of the set of 4 digits, but to do that, we must create the table of the set of 3 digits. We go about this in the same manner as just described, but here we learn one new fact: we always count up and back down again, so after doing the 3! permutations, followed by the 4! permutations, we find we must do another 3! permutations before finally we begin the upper body of the permutations for 5. The pattern here then is: 3, 4, 3, 5. The pattern for 6! permutations is: 3, 4, 3, 5, 3, 4, 3, 6 and the pattern for 7! permutations is 3, 4, 3, 5, 3, 4, 3, 6, 3, 4, 3, 5, 3, 4, 3, 7. Each successive factorial has a series that is twice as long as the previous.
For example, suppose we want all permutations for the set of 10 digits (0,1,2,3,4,5,6,7,8,9). This table will be 10! in total length, but the differences for first subset of permutations will be the same as if there were only 3 digits (yielding a set of 5 differences), and it's next group of permutations will have the same differences as if there were 4 digits in the set (yielding a set of 23 differences), back to 3 digits, then its next group of permutations will have the same differences as if there were 5 digits in the set (yielding a set of 119 differences), and so on up to the set of all the differences n!-1 for a 10 digit set.
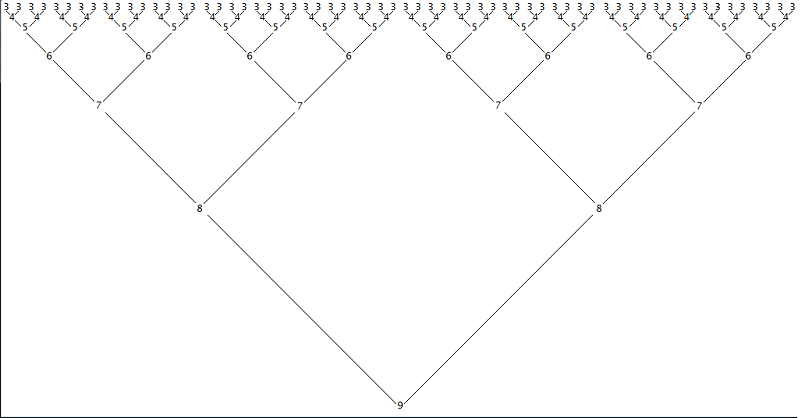
The following diagram illustrates all the subsets required leading up to developing the permutations for the set of 10 digits. Simply select the digit from each column reading across from left to right, regardless of which row it is in. Graphing it in this manner helps us to derive the function to generate them.

This pattern reveals the anatomy of the permutations of any set, no matter how large.
While creating all the n! permutations for the set n, we pause after generating each (1/2*factorial) + 1 permutations in each subset. To complete each subset, we add to the last generated permutation p the difference between it and the previous permutation p-1. The next permutation is derived from the difference between permutation p-1 and permutation p-2, and the next, from the difference between permutation p-2 and permutation p-3 and so on back to the start of the subset. Finally, we have a table of 1/2 n! + 1 permutations of the set n, which we complete in the same manner.
In the case where n is 5, for which the table of differences is displayed above, we can see that we are only required to call upon our permutation generating algorithm 41 times. The remaining 78 permutations are computed via addition to generate successive permutations.
Furthermore, if the set is compacted by bit-packing into for example, a 64 bit integer (or 128 bit integer on machines that support them), these bit-packed permutations can be directly subtracted. Though the individual values in the table of differences produced will be different, the same relationship holds true. It is much simpler to add and subtract integers than values stored in an array.
First let's take a look at the algorithm that adds the differences to compute permutations. The function below does not access differences stored in a table, but more illustratively, fetches previously generated permutations and subtracts them. It then adds the appropriate difference to the previous permutation to generate the next...
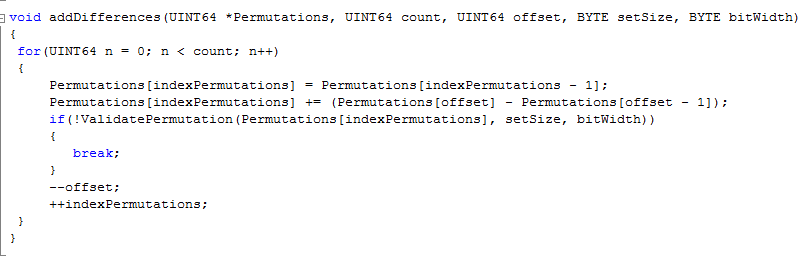
An offset was calculated before calling this function, pointing to the location in the array where the second last permutation generated is stored. In subsequent iterations the offset will be decremented to get the difference of each permutation going on back through the permutation table as new permutations are calculated. The source code supplied with this paper does an extra step, validating each permutation generated by the algorithm presented here with a permutation generated independently by conventional means.
Now we are ready to look at the recursive function that does all the work...

It is this function which traces out the fractal illustrated above. The first thing it does is recurse down to the lowest level and begin generating the subsets. It generates permutations unique to the set via whatever lexicographical algorithm you prefer, to arrive at 1/2 * n! + 1 permutations. When we have half the permutations, we only need to generate the other half via additions of the differences. It then calculates an offset to the second last permutation generated and calls addDifferences() where the remaining permutations of the subset are calculated via additions using a reflection of the difference table. For subsets larger than 3 we enter if(digits > 3). Here we encounter the final detail of the algorithm. The trick is that after each subset, we need to generate one more permutation before we go on to the next subset. This we call a "singleton", and it has an unique property in that it involves the reordering of nearly all the digits in the set, from near the first, and always to the last.
The table is an important part of the optimization. It is recommended that you use a table to store at least the first (n-1)! - 1 differences, because they will be used more than once. In fact, the table of differences for the first subset of 3!-1 for the generation of the permutations of just a 10 digit set will be accessed 64 times. It would pay to keep the series 9, 81, 18, 81, 9 handy on the stack. The 23 differences for the 4 digit subset will be used 32 time in this example, and each greater subset will use half that number again. The cost of creating a table then can be amortized over many accesses, and thereby becomes very cheap.
Using bit-packed integers to enumerate the permutations of a set of 12 digits, this algorithm with a table was, as expected, more than twice as fast when tested against the chosen permutation generator alone, even when it did nothing else with that permutation. The time in this test was approximately 17 seconds versus 36 seconds.
However, there is a down side. It is unlikely that it really matters if it took 17 seconds or 36 seconds, either is a short time to wait. Where we really want an optimization is when we are working with big sets, dozens or even hundreds of digits. 12 or 13 digits is pretty much the most one can do with this algorithm while maintaining the table in memory. Using the best memory compacting techniques, one would be lucky to do 13 digits with 12 Gb of ram installed. 14 digits would take at least 14 times the amount of ram. Therefore, for anything over 12 or 13 digits, we would have to swap the table data in and out from disk as needed. That would be thousands of times slower than a table in ram, and no optimization at all.
Now it is not quite that bad. We can use as much of a table as we have room for and gain some boost in speed from that. For example, repeating the above experiment, only this time with a set of 13 digits, the old table size for 12 digits was created and used. This gave us the permutations for the 13 digit set in approximately 7.7 minutes versus 8.1 minutes, a difference of 30 seconds. Giving the table 6 Gb of memory brought the time down to 6.8 minutes, 16% less time. That is significant, but the potential for optimization decreases exponentially as set size increases.
There is a way to optimize the table so that it requires less than half the space. This is possible because the table as described above contains much redundant information. Another advantage of the optimized version of the table is that it increases the number of permutations that can be calculated with a simple addition. Using this table with 13 digits brought the run time down to just 5.4 minutes, even though we can only use a partial table with 6 GB out of ram the 8 Gb that our development platform offers. That was 33% faster than not using this meta algorithm. I would say that was a very worthwhile optimization. There is a drawback to this though. A partial table must hold at least (n-1)! differences. It cannot be arbitrarily smaller like the first table can be.
This optimized table is created using a small stack that keeps track of the number of digits of each subset as they are created. Only the first half plus one of each subset is stored. Because of the top to bottom symmetry of each subset, the bottom half can be created as a reflection of the top half on demand. The use of a stack (of bytes) permits us to create the reflection of each subset as we go, and the final reflection of the entire remaining half of the n! permutations. Furthermore, it was found that the really big difference values that may require a 64 bit integer are the "singletons", described above. Since these are relatively very few in number, they are not saved on the table, but rather, regenerated as required. After doing this, we find that very few difference values up to the permutations for the 13 digit set require 64 bit integers. These rare values can be stored in a small supplementary table of big ints, while the table itself can be stored as double word values (32 bits). Whenever a 64 bit integer is encountered, the lo word (lower 16 bits) of the table value are zeroed as a flag, and the address in the supplemental table is stored in the hi word (upper 16 bits). Suddenly the table has gotten a whole lot smaller. This table could be saved to disk, and brought back in at will to regenerate all the permutations in the blink of an eye via simple addition for each and every permutation. Thus we could compact millions of permutations down to a small fraction of their original space requirements.
One further advantage of the optimized table is that it becomes a wonderful tool for exploring the number space. With it, we know where we are in terms of the subsets at all times, and can begin to investigate recurring phenomenon, like what kinds of swaps are happening, for example when the singletons referred to above are generated. This can lead to even further insights. With this stack-based approach, we can see that the difference table for 5 digits, for example, has this pattern: 3, 4, 3, 1, 3, 5, 3, 1, 3, 4, 3 in fine detail which isn't visible in the algorithm above because the entire reflection of current subsets is is done in one run through the table. In this pattern each 1 represents a singleton, and all the other numbers represent the subset number of digits - ie: the same pattern of differences that would be produced by the differences of the permutations of that number of digits. We may build a better permutation generator with that knowledge, perhaps one that uses the recursive function shown above and knowledge of each current subset to generate permutations even faster. Finally, we could begin to explore the rich details in fractal structure of the main body of each set, divorced from its preceding and subsequent subsets.
Up to now we have been talking about using digits bit-packed into integers, but they are not very useful in this form, as they would have to be unpacked each time to use them. We would prefer an optimization that permits us to maintain the digits of the permutations in a simple array. Addition with the differences did not yield an optimization in this case because it was faster to just swap digits as the existing permutation algorithms do. We investigated a different method for working with arrays. Using our insights into the fractal pattern discussed above, we examined Narayana's algorithm from this perspective. This algorithm iterates through the current set to find two indexes, 'k' and 'l', that will delineate the current group of digits to be shuffled. Observation of the first, 'k', revealed that it followed the now familiar pattern when generating the permutations for each subset. Specifically, it demonstrated exactly the same symmetry that the differences do. Then a table of these indexes could be stored and employed, frequently eliminating the need to derive 'k' via iterating in a loop. More than half the time, that step could be eliminated by passing the value to Narayana's algorithm instead. This resulted in a run time 25% faster for 13 digits, which required only 2.6 Gb of table space. That is a compelling result, indicating this meta-algorithm should be considered anywhere a dozen or so permutations in lexicographical order are required. Here is source code demonstrating this method.
In the end, no matter how much smaller the table, it still grows exponentially with each step up in number of digits in the set. There is no way to escape this mathematical law using a table. Even the new, optimized tables don't help us much in generating the permutations for the 14 digit set because it would require a platform with more ram than is practical, even for a partial tables. Even on industrial strength hardware a table is only practical for up to 15 digits.
However, there is a way to take advantage of the structure of the differences discussed here to gain nearly the same benefit as discussed using no table at all, if we accept bit-packed integers and an algorithm that generates two lists of permutations, one being the first half of all permutations in lexicographic order, and the remainder in reverse lexicographic order. Best of all, it will work with a set of any number of digits! If they are to be written to an array, the offsets can be easily calculated such that they all end up in lexicographic order, or they can be intermixed if that is not important. All we need to do this is begin with the original set, (0, 1, 2, ..., n-1) and the reverse of that set (n-1, ..., 2, 1, 0). Then as we generate each permutation for the first list, using the algorithm of your choice, we employ the difference between that and the previous to permute the second set. After we complete the first half, the second is all done.
Here is the full source code for creating permutations with bit-packed integers of variable bit width. And here is the source code applying this algorithm to array-based integers for comparison. Here is a table-based version. Finally, here we have code that employs the optimal table.
In the discussion above, we examined the table of differences between permutations in lexicographical order. Not only did we discover their fractal nature, but also learned how we can take advantage of that knowledge to simplify the generation of permutations. In the process, we discovered that to do that, we generate a series that in itself is fractal.
As far as we know, this algorithm is unique, and it is our own original invention. It can be proven by logical deduction alone, without depending on the carefully validated source code. On the surface it appears to be a breakthrough.
This algorithm is definitely the choice wherever one needs to compute permutations for sets of up to 13 digits as fast as possible. Unfortunately the table based version is of little or no use beyond that except on machines with an enormous amount of ram. However, a method was discussed that permitted optimization of permutation generation of sets of any number of digits, with no table needed and almost the same benefits. In the end though, even if this algorithm is of limited value, it may stimulate thinking towards further optimizations.
Now we sit back for a moment and contemplate the permutations themselves. They must comprise a fractal set as well. However, how to get a better visualization of a table of permutations so we can see this better?
In the first place, these numbers are often too big to grasp - too many digits. There is a simple way to cut them down to size when we realize they are in ascending order. Any table of permutations begins with the original set it was seeded with. For example, if we wanted the permutations for the set (0,1,2,3), we begin with 0123, and the remainder of the table is 0132, 0213, 0231, 0312, 0321, 1023, 1032, 1203, 1230, 1302, 1320, 2013, 2031, 2103, 2130, 2301, 2310, 3012, 3021, 3102, 3120, 3201, 3210.
These numbers are all "elevated" by the original base set, 0123. We could subtract 0123 from each and still have the same pattern. We would get (0132 - 123) = 0, (0213 - 123) = 90, (0231 - 123) = 108, etc. and very quickly we would notice something else, if we didn't already notice that when we were working with the table of differences. They are all evenly divisible by 9. Then each remainder of that previous operation could be divided by 9 to compact those permutations further, and still maintain the same pattern - like so: (0 / 9) = 0, (90 / 9) = 10, (108 / 9) = 12, etc.
Then when we were done we would have: 0, 1, 10, 12, 21, 22, 100, 101, 120, 123, 131, 133, 210, 212, 220, 223, 242, 243, 321, 322, 331, 333, 342, 343. Now we can see what we have. We also know that any time we want, we could restore those numbers to the original permutations by simply reversing the process - multiply by 9 and add the base (in this case, 123). We may contemplate that pattern 0, 1, 10, 12, 21, 22, etc. and speculate on how this can help us. Maybe we could generate such a series directly using recursion? Interesting thought, isn't it? While we are thinking about these numbers, let's examine another set and see what kind of pattern it creates, like the set of permutations for a 5 digit set - the next step up. Now there are 120 permutations in this set, so I won't list them all. How about I just list the first 24? They are: 01234, 01243, 01324, 01342, 01423, 01432, 02134, 02143, 02314, 02341, 02413, 02431, 03124, 03142, 03214, 03241, 03412, 03421, 04123, 04132, 04213, 04231, 04312, 04321, 10234.
What will we get when we process them as we did with the the 4 digit set? Just subtract the base, 01234, and divide the remainder by 9 for each and we get: (01234 - 1234) = 0, (0/9) = 0; (01243 - 1234) = 9, (9/9) = 1; (01324 - 1234) = 90, (90/9) = 10 and so on. In the end we have: 0, 10, 12, 21, 22, 100, 101, 120, 123, 131, 133, 210, 212, 220, 223, 242, 243, 321, 322, 331, 333, 342, 343.
Now compare the first 24 values with the table created by passing the permutations of the 4 digit set through the same process. They are identical! Then we know that we can create the first 24 permutations of the 5 digit set from that 4 digit set table of processed permutations by simply multiplying by 9 and adding the appropriate base from the 5 digit set (01234). After having read the first part of this discussion, we can leap to the conclusion that the first (n-1)! permutations of n digits can be directly derived from the permutations of the set of n-1 digits, by simply processing those permutations as we have just demonstrated and reconstituting them into the permutations of the n digit set, by multiplying by 9 and adding the appropriate base (0,1,2,...,n) of the n digit set. This is just another way of proving what we discovered in the first part of this paper. Beyond that, what else have we gained? Not much, but we have discovered another way of storing any table of permutations. We speculate that there may yet be a way of directly generating this series 0,1,10,12,21,22, etc, derived from processing the permutations of any set, with simple recursion.