Hungarian translation courtesy of Lera Domartina
Indonesian translation courtesy of Jordan Silaen
Urdu translation courtesy of Samuel Badree
Art or science?
I discovered this curious but probably completely useless algorithm in the fall of 1999. I even sent off a note to Dr. Dobb's Journal about it, and was delightfully surprised when they wrote back some months later and suggested I do an article for them. I was too busy at the time, and the world lost an opportunity for an incremental increase in useless knowledge. I am presenting this now; my gift to the world and perhaps my only legacy. Who knows maybe some mathematician working away in some dusty office may find it a keystone to solving some obscure theory.
The idea is very simple. Start with a screen populated with coloured pixels, randomly distributed. The number of possible colours doesn't matter, but it makes a more interesting image in the end if fewer colours are used. Then we begin sorting the pixels according to the following algorithm:
LOOP
For a screen of dimensions W, H
Pick a pixel at random coordinates x, y where x = {0 thru (W - 1)}, y = {0 thru (H - 2)}
If amount of red in pixel below (at x, y+1) is greater than red in current pixel, swap pixels
Pick another pixel at random coordinates x, y where x = {0 thru (W - 2)}, y = {0 thru (H - 2)}
If amount of green in pixel to the lower right (at x+1, y+1) is less than green in current pixel, swap pixels
Pick another pixel at random coordinates x, y where x = {1 thru (W - 1)}, y = {0 thru (H - 2)}
If amount of blue in pixel to the lower left (at x-1, y+1) is less than blue in current pixel, swap pixels
if(!done)goto LOOP
We continue looping like this millions of times, until an equilibrium becomes established in which colours are sorted into pools. The pixels of pure colour within the pools become immobile, and the only action that continues after that is some interplay along the interfaces of the colour pools.
As a generalized way of examining this phenomenon, imagine a given pixel with a determined amount of red, green, and blue. Depending on its red content, it experiences a force moving it up or down the screen, and depending on the amount of each of the other two colours, it experiences forces moving it diagonally left and right. Its final resting position is the vector sum of these three forces, in relation to all the other pixels on the screen. This sorting algorithm can be taken to even higher dimensions, and can be applied to any combination of properties, not just the colours of pixels. However, in any scenario I can imagine, conventional sorting techniques are far simpler and faster. If you find some use for this algorithm beyond creating psychedelic images, please let me know and please at least credit me for the idea.
3DSort.exe for the PC - WinZipped (26.6 Kb) is my latest Windows' GDI version (16 Feb 2004), which does the sort on various surface shapes (square, round, torus, etc.) in < 2 minutes for an area 512 pixel squared, and just seconds for an area 256 pixels squared. Optimized in assembler, it probably doesn't get any faster than this - at least on a P4 - 2 ghz platform, anyhow. Here are some images produced by it: Circle.gif, Triangle.gif, Torus.gif.
...
Update Aug 2016
Below is an image generated by creating 1024 separate images and averaging them all together. A total of 123 colours was used, generated by stepping each r, g, & b value by 64 and eliminating the colours black and white. An image size of 1024 x 632 was chosen because the ratio of width to height is equal to the Golden Ratio for a nice presentation.
Here is the code at the heart of that massive sorting job
Each image took just over two minutes to render, and the final resulting image required some 34.5 hours of processing time with an Intel i5 processor and lots of RAM. The point of the exercise was to find the "perfect sort" in the Platonic sense, since image generation depends entirely on random processes. It is interesting to note that even after averaging together all those randomly generated images, the resulting image still has sharp features, as if pixels are "predestined" to find their way to their final resting place. Well, maybe I just had too much time on my hands :)
...
Update Jan 2018
The next image below was produced the same way, but with 6 of the colours derived from a different palette. The use of different colours creates a totally different pattern. It required 17.5 hours of processing with an Intel i7-7700 CPU to render.
The next image below was produced the same way, but with 12 the colours derived from a different palette.
The next 3 images below were produced the same way. The first image on the right used 24 colours, the next used only 6 colours, and the last used 60 colours. The middle image used a different palette than the others.
...
The sort can be done in any number of dimensions. A sort was done on a cube 256 pixels on a side, populated with randomly distributed coloured pixels. There were 123 colours in all. The pixels were sorted according to the following algorithm...
LOOP
For a cube of dimensions W (width), H (height), D (depth)
Pick a pixel at random coordinates x, y, z where x = {0 thru (W-1)}, y = {0 thru (H-2)}, z = {0 thru (D-1)}
If amount of red in pixel below (at x, y+1, z) is greater than red in current pixel, swap pixels
Pick another pixel at random coordinates x, y, z where x = {0 thru (W-2)}, y = {0 thru (H-2)}, z = {0 thru (D-1)}
If amount of green in pixel to the lower right (at x+1, y+1, z) is less than green in current pixel, swap pixels
Pick another pixel at random coordinates x, y, z where x = {1 thru (W-1)}, y = {0 thru (H-2)}, z = {0 thru (D-1)}
If amount of blue in pixel to the lower left (at x-1, y+1, z) is less than blue in current pixel, swap pixels
Finally, pick a pixel at random coordinates x, y, z, where x = {0 thru (W-1)}, y = {0 thru (H-1)}, z = {0 thru (D-2)}
If the luminance value of the pixel behind at (at x, y, z+1) is greater than luminance value of current pixel, swap pixels.
Luminance or 'Y' is calculated as (0.299 * Red) + (0.587 * Green) + (0.114 * Blue)
if(!done)goto LOOP
Continue looping like this billions of times, until an equilibrium becomes established in which colours are sorted into blobs. The pixels of pure colour within the blobs become immobile, and the only action that continues after that is some interplay along the interfaces of some of the coloured blobs.
Now journey through a cube 256 pixels on a side, of pixels randomly assigned with 123 colours, sorted via this algorithm...
...
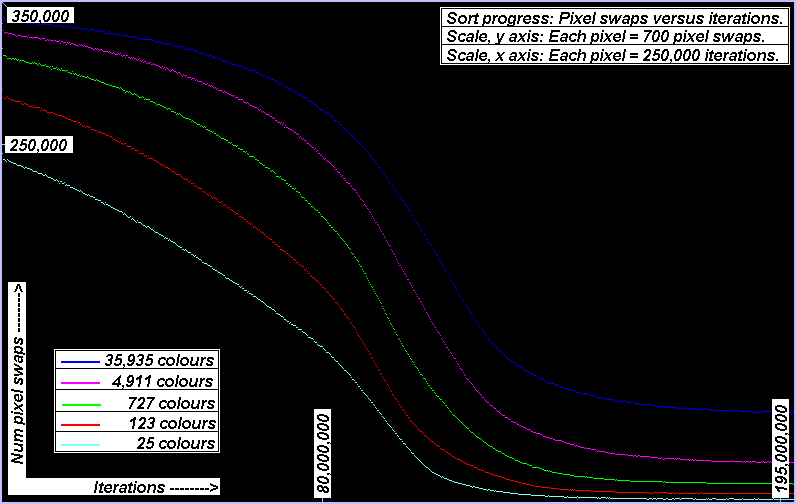
Below is a graph that illustrates progress during the sort for various numbers of colours on a square 512 pixels on a side. It can take almost 200 million iterations to reach a steady state. My first versions years ago took over two hours to do the sort. Only with today's P4 processors and hand-optimized assembler code can the sort be now done in a couple of minutes instead of hours. It can be seen that number of colours doesn't make a lot of difference as to when the algorithm reaches a steady state, where the colours are sorted as much as they can be. The only dramatic difference is that with more colours, more pixels are left to forever wander along the interfaces without a home to call their own.
The colours were derived by stepping each red, green, and blue colour component by 128, 64, 32, 16, or 8, then removing the black, white, and grays from the resultant colours for purely aesthetic reasons. This yields 25, 123, 727, 4,911, and 35,935 colours respectively.
